Korrelation und Kovarianz sind eng miteinander verbundene Begriffe in der theoretischen Statistik. Sie sind wichtig für die Bestimmung der Beziehung zwischen zwei Zufallsvariablen.
Was ist Korrelation?
Die Korrelation ist ein Maß für die Stärke der Beziehung zwischen zwei Variablen. Der Korrelationskoeffizient quantifiziert das Ausmaß der Veränderung einer Variablen in Abhängigkeit von der Veränderung der anderen Variablen.
In der Statistik steht die Korrelation im Zusammenhang mit dem Konzept der Abhängigkeit, also der statistischen Beziehung zwischen zwei Variablen.
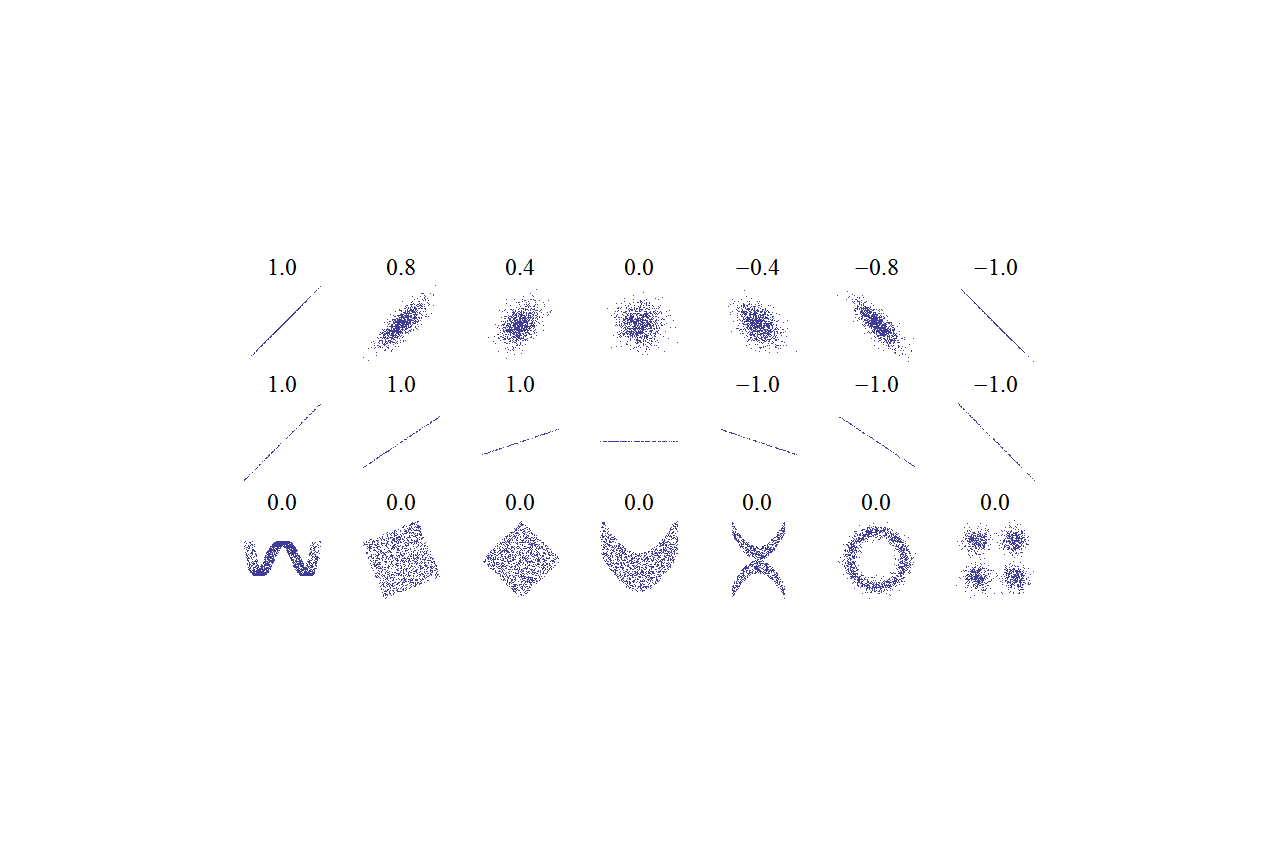
Der Pearsonsche Korrelationskoeffizient oder einfach der Korrelationskoeffizient r ist ein Wert zwischen -1 und 1 (-1≤r≤+1). Er ist der am häufigsten verwendete Korrelationskoeffizient und gilt nur für eine lineare Beziehung zwischen den Variablen.
Wenn r=0 ist, besteht kein Zusammenhang, und wenn r≥0 ist die Beziehung direkt proportional. Der Wert der einen Variablen steigt also mit dem Anstieg der anderen.
Ist r≤0, ist die Beziehung umgekehrt proportional. Der Wert der einen Variablen nimmt ab, wenn der Wert der anderen zunimmt.
Aufgrund der Linearitätsbedingung kann der Korrelationskoeffizient r auch verwendet werden, um das Vorhandensein einer linearen Beziehung zwischen den Variablen festzustellen.
Was ist Kovarianz?
In der statistischen Theorie ist die Kovarianz ein Maß dafür, wie stark sich zwei Zufallsvariablen gemeinsam verändern. Mit anderen Worten, die Kovarianz ist ein Maß für die Stärke der Korrelation zwischen zwei Zufallsvariablen.
Aus einem anderen Blickwinkel betrachtet, ist die Korrelation lediglich die normalisierte Version der Kovarianz, bei der die Kovarianz durch das Produkt der Standardabweichungen der beiden Zufallsvariablen geteilt wird.
Der Bereich der Kovarianz kann sehr groß sein und ist daher nicht einfach zu vergleichen. Diese Schwierigkeit wird überwunden, indem die Kovarianzwerte durch Normalisierung in einen vergleichbaren Bereich gebracht werden (ähnlich wie beim z-Score).
Obwohl die Kovarianz und die Varianz auf die oben beschriebene Weise miteinander verbunden sind, sind ihre Wahrscheinlichkeitsverteilungen nicht auf einfache Weise miteinander verbunden und müssen getrennt behandelt werden.
Was ist der Unterschied zwischen Korrelation und Kovarianz?
- Sowohl die Korrelation als auch die Kovarianz sind Maße für die Beziehung zwischen zwei Zufallsvariablen. Die Korrelation ist das Maß für die Stärke der Linearität der beiden Variablen und die Kovarianz ist ein Maß für die Stärke der Korrelation.
- Die Werte des Korrelationskoeffizienten liegen zwischen -1 und +1, während der Bereich der Kovarianz nicht konstant ist, sondern entweder positiv oder negativ sein kann. Wenn die Zufallsvariablen jedoch vor der Berechnung der Kovarianz normalisiert werden, ist die Kovarianz gleich der Korrelation und hat einen Wert zwischen -1 und +1.