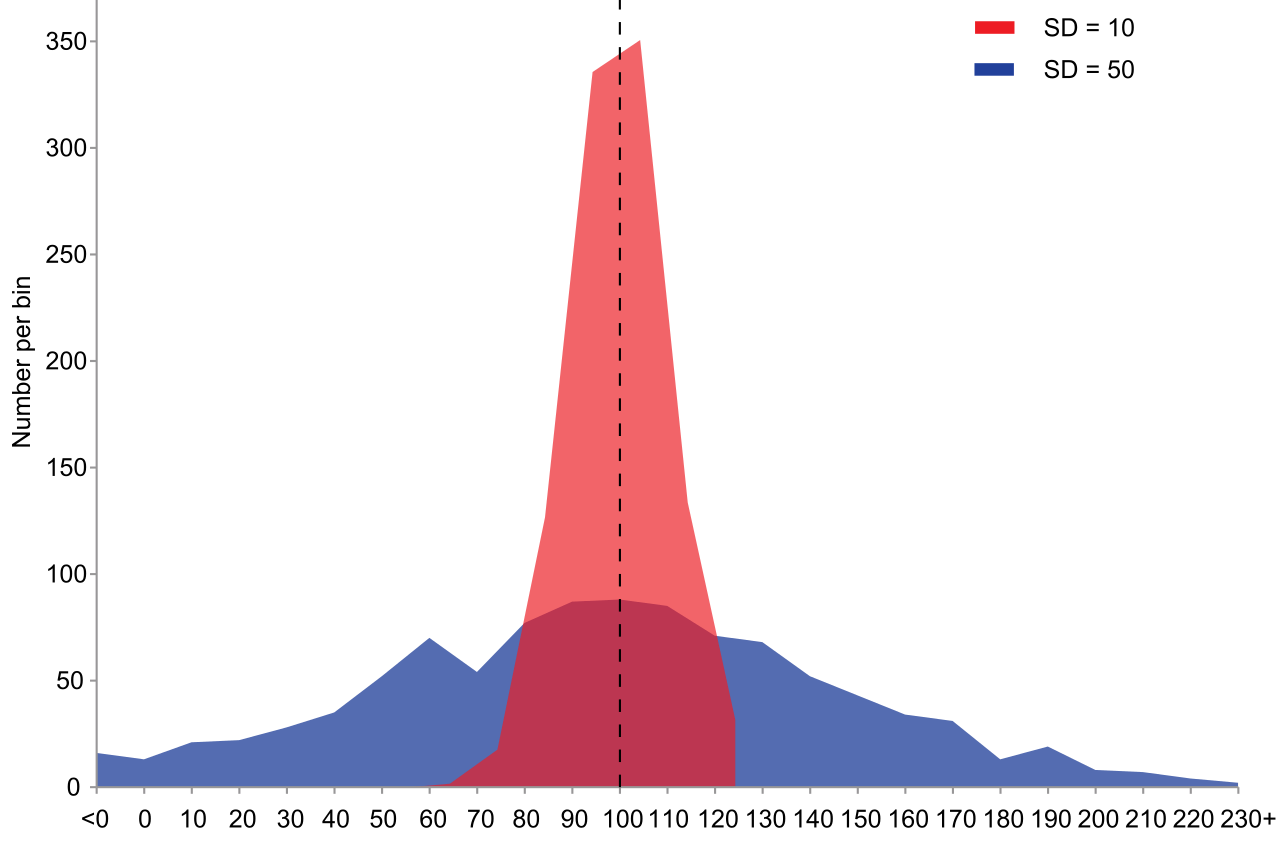
Varianz und Kovarianz sind zwei Maße, die in der Statistik verwendet werden.
Die Varianz ist ein Maß für die Streuung der Daten, und die Kovarianz gibt den Grad der Veränderung zweier Zufallsvariablen zusammen an.
Die Varianz ist ein eher intuitives Konzept, aber die Kovarianz ist mathematisch definiert und auf den ersten Blick nicht so intuitiv.
Was ist Varianz?
Die Varianz ist ein Maß für die Streuung der Daten gegenüber dem Mittelwert der Verteilung. Sie gibt an, wie weit die Datenpunkte im Schnitt vom Mittelwert der Verteilung entfernt liegen.
Sie ist einer der wichtigsten Deskriptoren der Wahrscheinlichkeitsverteilung und eines der Momente der Verteilung.
Die Varianz ist auch ein Parameter der Grundgesamtheit, und die Varianz einer Stichprobe aus der Grundgesamtheit dient als Schätzer für die Varianz der Grundgesamtheit.
Aus einer manthematischen Perspektive ist sie definiert als das Quadrat der Standardabweichung. Im Klartext kann sie als der Durchschnitt der Quadrate des Abstands zwischen jedem Datenpunkt und dem Mittelwert der Verteilung beschrieben werden.
Folgende Formel dient zur Berechnung der Varianz.
Var(X)=E[(X-µ)2 ] für eine Grundgesamtheit, und
Var(X)=E[(X-‾x)2 ] für eine Stichprobe
Man kann diese Formel weiter vereinfachen, sie ergibt dann Var(X)=E[X2 ]-(E[X])2.
Die Varianz hat einige charakteristische Eigenschaften. In der Statistik wird sie häufig verwendet, um die Anwendung zu vereinfachen. Sie ist nicht-negativ, da sie das Quadrat der Abstände ist.
Der Bereich der Varianz ist jedoch nicht begrenzt und hängt von der jeweiligen Verteilung ab. Die Varianz einer konstanten Zufallsvariablen ist Null, und die Varianz ändert sich nicht in Bezug auf einen Ortsparameter.
Was ist Kovarianz?
In der statistischen Theorie ist die Kovarianz ein Maß dafür, wie stark sich zwei Zufallsvariablen gemeinsam verändern.
Mit anderen Worten, die Kovarianz ist ein Maß für die Stärke der Korrelation zwischen zwei Zufallsvariablen. Sie kann auch als eine Verallgemeinerung des Konzepts der Varianz zweier Zufallsvariablen betrachtet werden.
Die Kovarianz von zwei Zufallsvariablen X und Y, die gemeinsam mit einem endlichen zweiten Impuls verteilt sind, ist bekannt als σXY=E[(X-E[X])(Y-E[Y])].
Daraus ergibt sich, dass die Varianz ein Spezialfall der Kovarianz ist, wenn die beiden Variablen gleich sind, also Cov(X,X)=Var(X).
Durch Normalisierung der Kovarianz erhält man den linearen Korrelationskoeffizienten oder den Pearsonschen Korrelationskoeffizienten, der definiert ist als ρ=E[(X-E[X])(Y-E[Y])]/(σX σY )=( Cov(X,Y))/(σX σY).
Grafisch gesehen kann man die Kovarianz zwischen einem Paar von Datenpunkten als die Fläche des Rechtecks mit den Datenpunkten an den gegenüberliegenden Eckpunkten ansehen.
Man kann sie auch als Maß für die Größe des Abstands zwischen den beiden Datenpunkten interpretieren.
Betrachtet man die Rechtecke für die gesamte Population, so kann die Überlappung der Rechtecke, die allen Datenpunkten entsprechen, als Stärke der Trennung, d. h. als Varianz der beiden Variablen, angesehen werden.
Die Kovarianz ist zweidimensional, da es sich um zwei Variablen handelt. Aber die Vereinfachung auf eine Variable ergibt die Varianz einer einzelnen als die Trennung in einer Dimension.
Was ist der Unterschied zwischen Varianz und Kovarianz?
- Die Varianz ist das Maß für die Streuung in einer Population, während die Kovarianz ein Maß für die Variation zweier Zufallsvariablen oder die Stärke der Korrelation ist.
- Die Varianz ist ein Spezialfall der Kovarianz, also die Kovarianz einer Variablen mit sich selbst.
- Varianz und Kovarianz sind von der Größe der Datenwerte abhängig. Man kann sie nicht direkt miteinander vergleichen. Daher werden sie normalisiert. Die Kovarianz wird zum Korrelationskoeffizienten normalisiert, durch Division durch das Produkt der Standardabweichungen der beiden Zufallsvariablen. Die Varianz wird zur Standardabweichung normalisiert durch Ziehen der Quadratwurzel.